In the section on the Doppler effect we have only
considered cases where the source is moving with a speed less than the speed of the waves
(v < c). The problem of the case where v>c was solved by Mach in 1936 (he received the
Nobel Prize for Physics in 1958).
Consider a source S moving with velocity v (> c).
In one second the source will have moved from S to S', a distance v, and in that time the
waves will have moved from S to P, a distance c.
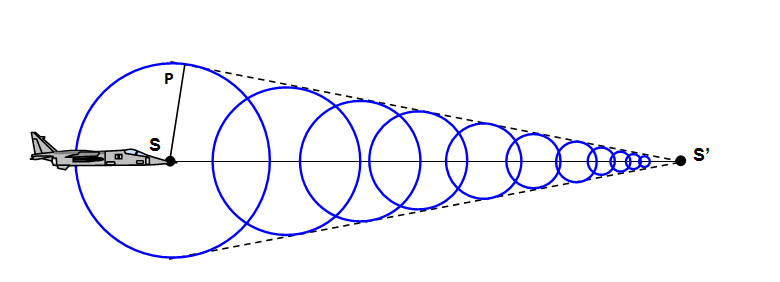

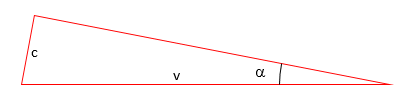
The envelope of the waves will be a cone
of semi angle a, where sin a, =
c/(v). (see Figure 2). The greater the value of v, the narrower the cone will be. In this case
v>c.
Examples of this are a sonic boom from an aircraft, the bow wave from a ship,
the mini sonic boom from cracking a whip and shock waves from a bullet.
The same
effect is also observed with light, as Cerenkov radiation. In some materials electrons from an
accelerator can move faster than the velocity of light in that material and as the electrons
travel through the solid or liquid a bluish radiation, a kind of shock wave, is observed, (for
example, in water-moderated nuclear reactors).